Hệ số góc là gì? Công thức tính hệ số góc và ứng dụng

I. Hệ số góc là gì?

– Hệ số góc, hay còn được gọi là độ dốc, là một chỉ số quyết định độ dốc của một đường thẳng hoặc đường cong. Nó cho biết mức độ tăng hoặc giảm của giá trị y đối với giá trị x trên đồ thị hoặc biểu đồ.

II. Công thức tính hệ số góc và ứng dụng.

– Hệ số góc (m) được tính bằng cách chia sự thay đổi trong giá trị y (Δy) cho sự thay đổi tương ứng trong giá trị x (Δx). Công thức này được biểu diễn như sau:

m = Δy/Δx.

Xem xét ví dụ sau để minh họa cách tính hệ số góc:
Hãy xem xét hai điểm trên đồ thị: A(1, 2) và B(4, 8).
Δy = 8 – 2 = 6
Δx = 4 – 1 = 3
m = Δy/Δx = 6/3 = 2

Trong trường hợp này, hệ số góc của đoạn thẳng AB là 2, cho thấy rằng đoạn thẳng nghiêng lên và tăng 2 đơn vị của y cho mỗi đơn vị tăng của x.

III. Ứng dụng trong hình học và đại số và các ứng dụng khác.

A. Hệ số góc của đường thẳng

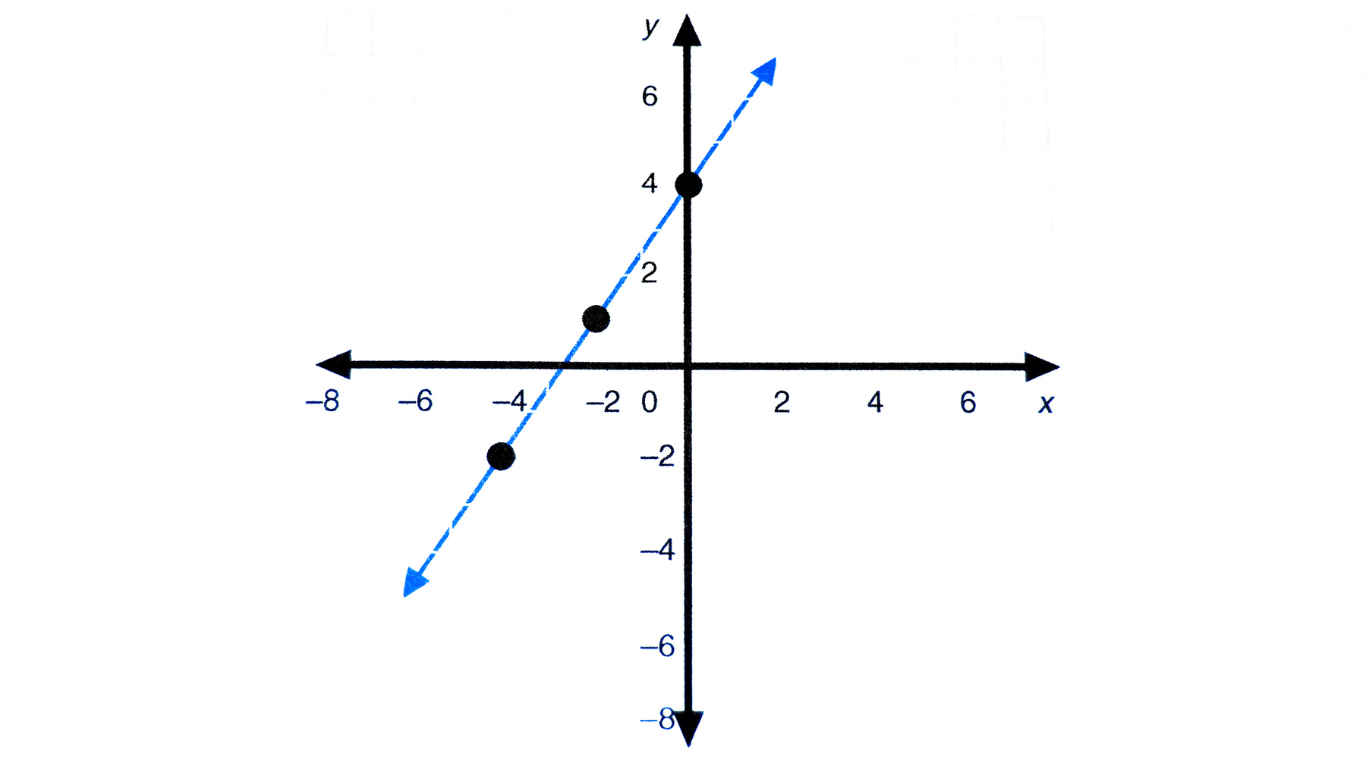
– Trong hình học, hệ số góc của đường thẳng định nghĩa độ dốc của đường thẳng đó. Điều này rất hữu ích để biết được cách đường thẳng nghiêng và hướng nghiêng đó là tăng hay giảm.

Ví dụ: Đường thẳng y = 2x + 3 có hệ số góc là 2, cho thấy độ dốc dương và tăng 2 đơn vị của y cho mỗi đơn vị tăng của x.

B. Hệ số góc của đồ thị hàm số

– Trong đại số, hệ số góc xuất hiện khi biểu đồ một hàm số. Nó cho biết tốc độ thay đổi của hàm số tại một điểm cụ thể và giúp ta hiểu sâu hơn về đồ thị của hàm.

Hãy xem xét hàm số y = 3x^2. Hệ số góc trong trường hợp này là 6x, tức là tốc độ thay đổi của y đối với x phụ thuộc vào giá trị của x. Ví dụ, khi x = 2, hệ số góc là 12, cho thấy tốc độ thay đổi của y là 12 đơn vị cho mỗi đơn vị tăng của x.

C.Đường dẫn giao thông:

Trên một con đường dẫn giao thông, một biển báo có thể hiển thị hệ số góc để cảnh báo tài xế về độ dốc của đường. Ví dụ, biển báo với hệ số góc dương có thể chỉ ra một đoạn đường dốc lên, trong khi hệ số góc âm có thể chỉ ra một đoạn đường dốc xuống.

D. Tài chính cá nhân:

Trong tài chính cá nhân, hệ số góc có thể áp dụng khi bạn đánh giá tốc độ tăng trưởng của đầu tư hoặc tiền gửi. Ví dụ, nếu một khoản đầu tư tăng 10% hàng năm, hệ số góc là 0.1 (10/100).

E.Hệ số góc và mối quan hệ xã hội:

Trong mối quan hệ xã hội, hệ số góc có thể áp dụng để đo lường sự thay đổi trong quan hệ giữa hai người hoặc một nhóm. Ví dụ, nếu một người có thể thấy rằng thời gian họ dành cho một người bạn giảm dần theo thời gian, họ có thể nói rằng hệ số góc của mối quan hệ này đang giảm.
Hệ số góc và tốc độ thay đổi của sự kiện:

Trong khoa học, hệ số góc có thể áp dụng để đo lường tốc độ thay đổi của biến số trong quá trình nghiên cứu. Ví dụ, nếu bạn đo lường tốc độ tăng trưởng của một loài thực vật trong một nghiên cứu sinh học, hệ số góc sẽ giúp bạn hiểu tốc độ tăng trưởng này.

IV. Hệ số góc trong cuộc sống hằng ngày

A. Đường dẫn giao thông

Có thể áp dụng vào việc đánh giá độ dốc của đường khi lái xe. Điều này quan trọng để an toàn giao thông và quản lý tốc độ.

B. Tài chính cá nhân

Trong tài chính cá nhân, nó có thể áp dụng để đo lường tốc độ tăng trưởng của đầu tư hoặc tiền gửi. Nó giúp xác định lợi nhuận dự kiến từ một khoản đầu tư.

C. Quản lý thời gian

Nó cũng có thể liên quan đến quản lý thời gian. Nó giúp xác định mức độ tăng hoặc giảm của hiệu suất công việc theo thời gian và từ đó cải thiện hiệu suất làm việc.

D. Mối quan hệ xã hội

Nó cũng có thể áp dụng trong mối quan hệ xã hội để đo lường sự thay đổi trong quan hệ và tốc độ phát triển của mối quan hệ.
Ví dụ, trong mối quan hệ tình yêu, hệ số góc có thể đại diện cho tốc độ tăng hoặc giảm của tình cảm giữa hai người. Nếu hệ số góc là dương, tình cảm có thể đang phát triển tốt; nếu là âm, có thể có sự giảm đi trong mối quan hệ và cần xem xét các điều chỉnh.
Hệ số góc không chỉ là một khái niệm trong toán học mà còn có ứng dụng rộng rãi trong nhiều khía cạnh của cuộc sống hằng ngày và có thể giúp chúng ta hiểu sâu hơn về tốc độ thay đổi và độ dốc của các quy trình và quan hệ.

V. Hệ số góc trong khoa học và công nghệ

A. Ứng dụng trong công nghệ thông tin

Có thể sử dụng trong thuật toán và phân tích dữ liệu để đo lường tốc độ thay đổi của thông tin hoặc hiệu suất của hệ thống.

B. Hệ số góc là gì trong nghiên cứu khoa học

-Trong nghiên cứu khoa học, nó có thể áp dụng để đo lường tốc độ thay đổi của biến số trong quá trình nghiên cứu.

C. Các ứng dụng tiềm năng

Nó có tiềm năng trong nhiều lĩnh vực, từ robot học, trí tuệ nhân tạo đến phân tích dữ liệu và dự đoán trong tài chính.

VI. Hệ số góc và phát triển cá nhân:

A. Sự quan trọng của hiểu biết về hệ số góc:

Hiểu biết về hệ số góc có thể mang lại nhiều lợi ích cho phát triển cá nhân:
Tư duy phân tích: Hiểu biết về nó giúp bạn phát triển tư duy phân tích, khả năng xem xét tương quan và mối quan hệ giữa các biến số.
Ra quyết định thông minh: Khi bạn thấu hiểu hệ số góc, bạn có thể đưa ra quyết định thông minh dựa trên sự hiểu biết về tốc độ thay đổi của các yếu tố quan trọng.
Giải quyết vấn đề: Sử dụng hệ số trong việc giải quyết vấn đề có thể giúp bạn tiếp cận các tình huống phức tạp một cách cấu trúc và hiệu quả hơn

B. Làm thế nào để cải thiện khả năng sử dụng hệ số góc:

Để cải thiện khả năng sử dụng hệ số góc, bạn có thể thực hiện các bước sau:
Học cơ bản: Để đầu tiên, bạn cần hiểu cơ bản về hệ số góc, cách tính toán nó và ý nghĩa của nó trong các tình huống khác nhau.
Thực hành: Thực hành sử dụng hệ số góc trong các bài toán thực tế hoặc trong việc phân tích dữ liệu. Điều này giúp bạn làm quen với cách áp dụng kiến thức vào thực tế.
Học từ người khác: Nếu có cơ hội, học từ người có kinh nghiệm trong việc sử dụng hệ số góc. Chia sẻ ý tưởng và kinh nghiệm với họ để học hỏi.
Tìm tài liệu: Tìm tài liệu và sách về hệ số góc và các ứng dụng của nó trong lĩnh vực bạn quan tâm. Điều này có thể giúp bạn tiếp cận kiến thức sâu hơn.

C. Hệ số góc là gì  trong khả năng giải quyết vấn đề:

Hệ số góc có thể giúp trong quá trình giải quyết vấn đề bằng cách:
Hiểu rõ mối quan hệ: Hệ số góc giúp bạn hiểu rõ hơn về mối quan hệ giữa các yếu tố và tốc độ thay đổi của chúng. Điều này có thể dẫn đến sự nhận biết tốt hơn về nguyên nhân và hậu quả.
Dự đoán: Nắm vững hệ số góc cho phép bạn dự đoán tốc độ thay đổi tương lai, giúp bạn chuẩn bị và đưa ra các quyết định dựa trên thông tin dự đoán.
Giải quyết vấn đề phức tạp: Hệ số có thể được sử dụng để phân tích và giải quyết các vấn đề phức tạp hơn, từ quản lý dự án đến phân tích tài chính.
Tổng hợp lại, hiểu biết về hệ số góc không chỉ cung cấp kiến thức toán học mà còn là một kỹ năng quan trọng cho sự phát triển cá nhân và khả năng giải quyết vấn đề trong nhiều khía cạnh của cuộc sống và công việc.

VII. Hệ số góc trong khoa học và công nghệ:

A. Ứng dụng trong công nghệ thông tin:

Nó có rất nhiều ứng dụng trong lĩnh vực công nghệ thông tin:

Phân tích dữ liệu: Trong phân tích dữ liệu và khoa học dữ liệu, hệ số góc có thể được sử dụng để đo lường tốc độ thay đổi của dữ liệu theo thời gian. Điều này quan trọng trong việc xây dựng các mô hình dự đoán và phát triển các chiến lược dựa trên dữ liệu.
Thuật toán học máy: Trong máy học, nó có thể được sử dụng để tối ưu hóa mô hình. Ví dụ, trong hồi quy tuyến tính, tìm kiếm hệ số góc tốt nhất giúp mô hình phù hợp với dữ liệu tốt hơn.
Thị giác máy tính: Trong thị giác máy tính và xử lý ảnh, hệ số góc có thể giúp xác định góc nghiêng của các đối tượng hoặc đường thẳng trong hình ảnh, điều này hữu ích trong việc nhận dạng và theo dõi các đối tượng.

B. Hệ số góc là gì trong nghiên cứu khoa học:

Nó có thể được sử dụng trong nghiên cứu khoa học để đo lường tốc độ thay đổi của biến số trong quá trình nghiên cứu. Nó có thể áp dụng trong nhiều lĩnh vực khoa học như vật lý, hóa học, sinh học, và kỹ thuật.
Ví dụ:
Trong vật lý, nó có thể đại diện cho tốc độ thay đổi của vận tốc, gia tốc, hoặc các biến số khác liên quan đến chuyển động.
Trong sinh học, nó có thể sử dụng để đo tốc độ tăng trưởng của dân số, biến đổi trong gen, hoặc sự biến đổi của các tham số sinh học.

C. Các ứng dụng tiềm năng:

Hệ số góc có tiềm năng ứng dụng rộng rãi trong tương lai và có thể được sáng tạo và phát triển trong nhiều lĩnh vực:
Trí tuệ nhân tạo (AI): Có thể được sử dụng để cải thiện việc học máy và mô hình học sâu, giúp máy tính hiểu sâu hơn về mối quan hệ giữa các biến số.
Khoa học xã hội: Trong nghiên cứu xã hội, nó có thể được áp dụng để đo lường tốc độ thay đổi của các yếu tố xã hội như sự thay đổi trong hành vi người tiêu dùng, xu hướng xã hội, và sự thay đổi trong độc lập kinh tế.
Công nghệ sinh học: Trong lĩnh vực công nghệ sinh học, nó có thể giúp theo dõi tốc độ tăng trưởng của vi khuẩn, tế bào, hoặc quá trình sinh học khác có liên quan đến nghiên cứu dược phẩm hoặc y học.
Nó không chỉ là một công cụ toán học, mà còn là một khái niệm có ứng dụng sâu rộng trong nhiều lĩnh vực khoa học và công nghệ, từ máy tính đến nghiên cứu khoa học và sáng tạo trong tương lai.

IX. Lời kết.

Trong bài viết này, chúng ta đã tìm hiểu về khái niệm hệ số góc là gì và cách tính toán nó. Chúng ta đã thấy rằng nó không chỉ là một khái niệm toán học mà còn có rất nhiều ứng dụng trong cuộc sống hằng ngày, khoa học, công nghệ, và phát triển cá nhân. Nó giúp chúng ta hiểu sâu hơn về tốc độ thay đổi của các biến số và có thể được sử dụng để giải quyết nhiều vấn đề phức tạp.

Nếu bạn muốn biết thêm về cách sử dụng hệ số góc trong một lĩnh vực cụ thể hoặc có bất kỳ câu hỏi hoặc yêu cầu khác, xin hãy liên hệ. Chúc bạn thành công trong việc áp dụng hệ số

 

Các bạn có thể tham khảo thêm các bài viết khác tại đây.